Programme des exposés
| Date | Heure | Salle | Orateur | N° | Titre |
|---|---|---|---|---|---|
| 13 mai 2025 | 13h30–14h30 | E554 | Ruslan Maksimau | 1 | Qu’est-ce que le spin ? Introduction aux qubits [notes en PDF] |
| 27 mai 2025 | 13h30–14h30 | E554 | Louis Garrigue | 2 | Introduction au calcul quantique (sur un ordinateur quantique) |
| 3 juin 2025 | 13h30–14h30 | E554 | Louis Garrigue | 3 | Codes correcteurs quantiques |
| 23 juin 2025 | 15h15–16h15 | E532 | Ruslan Maksimau | 4 | Le formalisme des stabilisateurs pour les codes correcteurs quantiques [source] |
| 25 novembre 2025 | 16h30–17h30 | E532 | Jules Martel | 5 | Code torique de Kitaev 1 [source] |
| 2 décembre 2025 | 16h30–17h30 | E532 | Jules Martel | 6 | Code torique de Kitaev 2 [source] |
| 9 décembre 2025 | 16h30–17h30 | E532 | ?? | 7 | ?? |
| 16 décembre 2025 | 16h30–17h30 | E532 | ?? | 8 | ?? |
| La suite du programme sera précisée ultérieurement. | |||||
Introduction
Les ordinateurs quantiques utilisent des qubits pour traiter l'information de manière fondamentalement différente des ordinateurs classiques. Une des approches prometteuses est le calcul quantique topologique, basé sur la manipulation d'anyons — des quasi-particules qui apparaissent dans certains systèmes strictement bidimensionnels.
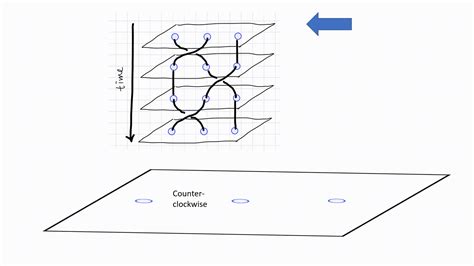
Pour les bosons et les fermions, lorsqu'on échange deux particules identiques, l'état quantique est multiplié respectivement par +1 ou −1. En revanche, pour les anyons, le résultat peut être un scalaire eiϕ (autre que +1 ou −1) dans le cas abélien. Dans le cas non-abélien, on peut obtenir un opérateur unitaire plus général lorsqu'un anyon tourne autour d'un autre. Cela est possible parce que les anyons vivent dans des systèmes strictement bidimensionnels.
Les anyons existent réellement dans certains matériaux réels, notamment dans les systèmes à effet Hall quantique fractionnaire. Leur manipulation permet de réaliser des opérations quantiques robustes contre les perturbations extérieures, ce qui est crucial pour le calcul quantique tolérant aux fautes.
Programme envisagé
- Exposé 1 : Qu'est-ce que le spin d'un point de vue mathématique ? Introduction aux qubits. [notes en PDF]
- Exposé 2 : Des exemples d'applications réalisables avec des ordinateurs quantiques.
- Exposés 3-4 : Codes correcteurs quantiques. Une référence parmi d’autres : arXiv:0904.2557
- Exposés 5, 6, 7... : Fault-tolerant quantum computation by anyons
https://www.sciencedirect.com/science/article/pii/S0003491602000180 - Les exposés 8, 9, ... (si nous arrivons jusque-là) : pourront s'adapter en fonction de nos intérêts. Une option intéressante serait d'explorer l'article récent de Lauda et al. :
arXiv:2410.14860
Les deux premiers exposés auront pour objectif de se familiariser avec le domaine des ordinateurs quantiques. Ils ne sont pas strictement nécessaires pour comprendre la suite, mais ils offriront une bonne vue d'ensemble du contexte.
Le troisième exposé est destiné à apprendre les concepts de base nécessaires pour aborder la partie principale.
Les exposés suivants porteront sur l'article fondateur de Kitaev :